CS61a Learning Note

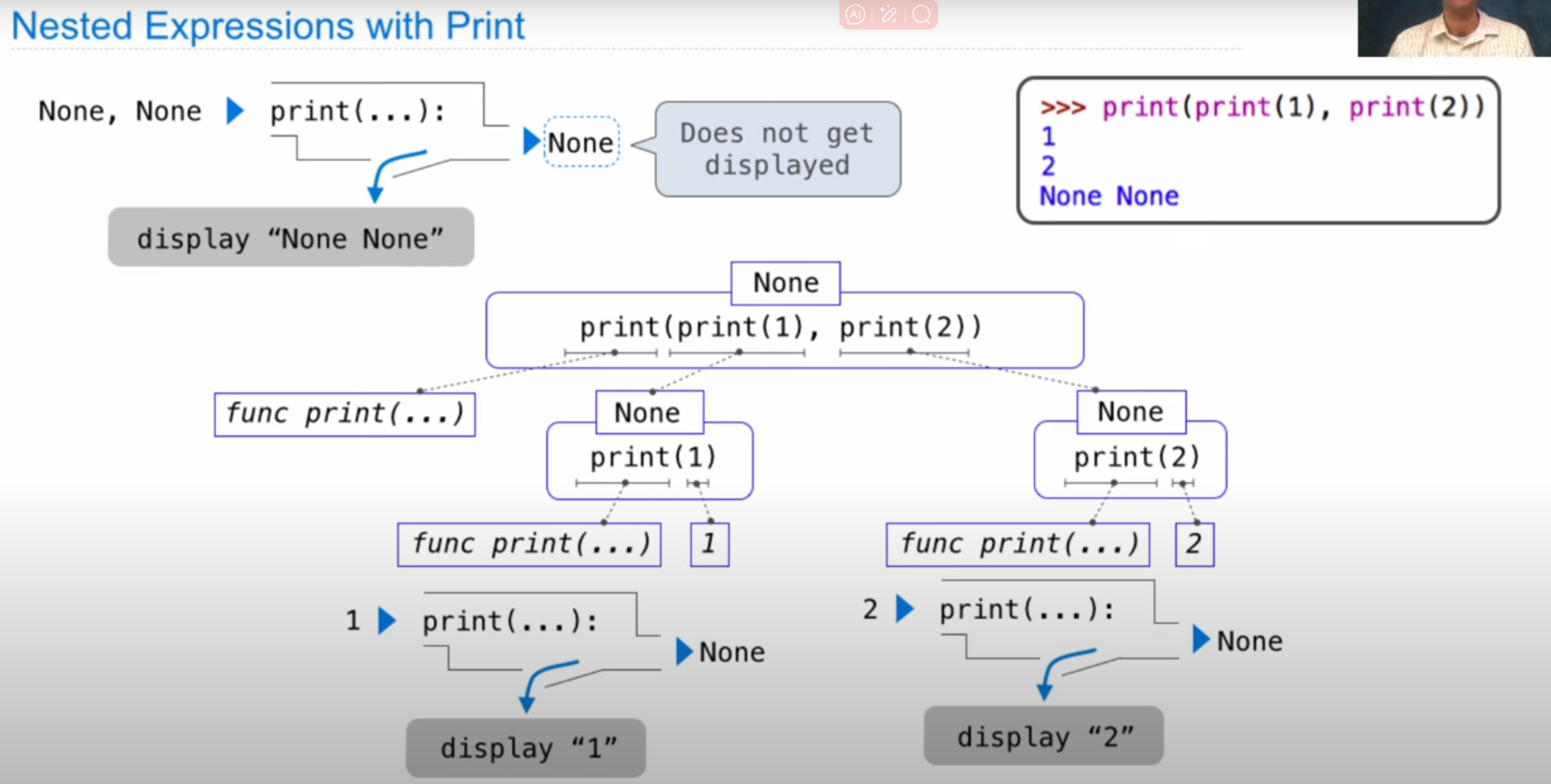
print(print(1),print(2))
```
1
2
None None
```
# print() is Non-Pure Functions

Casual Literary Notes

Note: When we say condition is a predicate function, we mean that it is a function that will return True or False.

Questions

Q5: Count Stair Ways

Imagine that you want to go up a flight of stairs that has n steps, where n is a positive integer. You can take either one or two steps each time you move. In how many ways can you go up the entire flight of stairs?

You’ll write a function count_stair_ways to answer this question. Before you write any code, consider:

How many ways are there to go up a flight of stairs with n = 1 step? What about n = 2 steps? Try writing or drawing out some other examples and see if you notice any patterns.

Solution: When there is only one step, there is only one way to go up. When there are two steps, we can go up in two ways: take a single 2-step, or take two 1-steps.

What is the base case for this question? What is the smallest input?

Solution: We actually have two base cases! Our first base case is when there is one step left. n = 1 is the smallest input because 1 is the smallest positive integer.

Our second base case is when there are two steps left. The primary solution (found below) cannot solve count_stair_ways(2) recursively because count_stair_ways(0) is undefined.

(virfib has two base cases for a similar reason: virfib(1) cannot be solved recursively because virfib(-1) is undefined.)

Alternate solution: Our first base case is when there are no steps left. This means we reached the top of the stairs with our last action.

Our second base case is when we have overstepped. This means our last action was invalid; in other words, we took two steps when only one step remained.

Solution: count_stair_ways(n - 1) is the number of ways to go up n - 1 stairs. Equivalently, count_stair_ways(n - 1) is the number of ways to go up n stairs if our first action is taking one step.

count_stair_ways(n - 2) is the number of ways to go up n - 2 stairs. Equivalently, count_stair_ways(n - 2) is the number of ways to go up n stairs if our first action is taking two steps.

Now, fill in the code for count_stair_ways:

Your Answer

Run in 61A Code

Solution

def count_stair_ways(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either one step or two steps at a time.
    >>> count_stair_ways(1)
    1
    >>> count_stair_ways(2)
    2
    >>> count_stair_ways(4)
    5
    """
    if n == 1:
        return 1
    elif n == 2:
        return 2
    return count_stair_ways(n-1) + count_stair_ways(n-2)

Here’s an alternate solution that corresponds to the alternate base cases:

def count_stair_ways_alt(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either 1 step or 2 steps at a time.
    >>> count_stair_ways_alt(4)
    5
    """
    if n == 0:
        return 1
    elif n < 0:
        return 0
    return count_stair_ways_alt(n-1) + count_stair_ways_alt(n-2)

You can use [Recursion Visualizer](https://www.recursionvisualizer.com/?function_definition=def count_stair_ways(n)%3A if n %3D%3D 1%3A return 1 elif n %3D%3D 2%3A return 2 return count_stair_ways(n-1) %2B count_stair_ways(n-2)&function_call=count_stair_ways(4)) to step through the call structure of count_stair_ways(4) for the primary solution.

You’re done! Excellent work this week. Please be sure to fill out your TA’s attendance form to get credit for this discussion!

Q6: Subsequences

A subsequence of a sequence S is a subset of elements from S, in the same order they appear in S. Consider the list [1, 2, 3]. Here are a few of its subsequences [], [1, 3], [2], and [1, 2, 3].

Write a function that takes in a list and returns all possible subsequences of that list. The subsequences should be returned as a list of lists, where each nested list is a subsequence of the original input.

In order to accomplish this, you might first want to write a function insert_into_all that takes an item and a list of lists, adds the item to the beginning of each nested list, and returns the resulting list.

Your Answer

Run in 61A Code

Solution

def insert_into_all(item, nested_list):
    """Return a new list consisting of all the lists in nested_list,
    but with item added to the front of each. You can assume that
    nested_list is a list of lists.

    >>> nl = [[], [1, 2], [3]]
    >>> insert_into_all(0, nl)
    [[0], [0, 1, 2], [0, 3]]
    """
    return [[item] + lst for lst in nested_list]

def subseqs(s):
    """Return a nested list (a list of lists) of all subsequences of S.
    The subsequences can appear in any order. You can assume S is a list.

    >>> seqs = subseqs([1, 2, 3])
    >>> sorted(seqs)
    [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
    >>> subseqs([])
    [[]]
    """
    if not s:
        return [[]]
    else:
        subset = subseqs(s[1:])
        return insert_into_all(s[0], subset) + subset